Berikut ini akan kita bahas gerak lurus berubah beraturan, GLBB, grafik glbb, contoh glbb, glbb dipercepat, contoh glbb dipercepat, glbb diperlambat, glbb fisika, contoh glbb dalam kehidupan sehari hari, gerak lurus berubah beraturan glbb, contoh glbb diperlambat, rumus glbb, contoh soal glbb.
Gerak Lurus Berubah Beraturan (GLBB)
Setelah Anda mempelajari materi mengenai gerak lurus beraturan, Anda tentu harus mengetahui bahwa tidak ada benda yang selalu dapat bergerak dengan kecepatan konstan. Sebuah benda yang bergerak tidak selalu memiliki kecepatan yang konstan dan lintasan yang lurus.
Dalam kehidupan seharihari, setiap benda cenderung untuk mempercepat dan memperlambat secara tidak beraturan.
Gerak lurus yang memiliki kecepatan berubah secara beraturan disebut gerak lurus berubah beraturan (GLBB). Benda yang bergerak berubah beraturan dapat berupa bertambah beraturan (dipercepat) atau berkurang beraturan (diperlambat).
Jika Anda perhatikan Gambar berikut ini, akan diperoleh sebuah persamaan percepatan, yaitu besarnya tangen α .
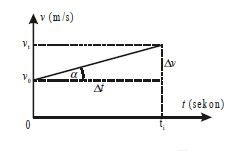 |
Grafik kecepatan terhadap
waktu untuk gerak lurus
berubah beraturan |
Dari persamaan percepatan rata-rata, diperoleh:
dengan Δv = vt – v0, vt adalah kecepatan akhir, v0 adalah kecepatan awal dan Δt = t – t0.
Oleh karena t0 = 0
Dengan mengalikan silang persamaan tersebut, akan diperoleh persamaan baru
dengan vt = kecepatan akhir, v0 = kecepatan awal, a = percepatan, dan t = waktu.
Contoh Soal 1:
Sebuah mobil bergerak dipercepat dari keadaan diam. Jika percepatan mobil 20 m/s2, tentukanlah kecepatan mobil tersebut setelah 5 sekon.
Untuk memperoleh besar perpindahan, dapat ditentukan dari persamaan kecepatan rata-rata.
Substitusikan Persamaan (3–7) ke dalam Persamaan (3–8), diperoleh
Contoh Soal 2:
Tonton Suprapto atlet balap sepeda Jawa Barat dapat mengayuh sepedanya dengan kecepatan awal 10 km/jam pada suatu perlombaan. Atlet tersebut dapat mencapai garis finish dalam waktu 2 jam dengan percepatan 20 km/jam2. Tentukanlah panjang lintasan yang ditempuh atlet tersebut.
Jika pada Persamaan (3–7) diubah menjadi persamaan waktu, diperoleh
Persamaan (3–10) disubstitusikan ke dalam Persamaan (3–9) maka
Contoh Soal 3:
Sebuah benda bergerak dengan percepatan 8 m/s2. Jika kecepatan awal benda 6 m/s, tentukanlah kecepatan benda setelah menempuh jarak 4 m.
Jadi, kecepatan akhir benda setelah menempuh jarak 4 m adalah 10 m/s.






