Berikut ini akan kita bahas mengenai penjumlahan vektor, besaran vektor, vektor fisika, penjumlahan vektor secara grafis, vektor grafis, vektor fisika kelas x, operasi vektor, penjumlahan vektor fisika, penjumlahan vektor secara analitis, cara menghitung resultan vektor, menentukan resultan vektor, resultan vektor, cara mencari resultan vektor, mencari resultan vektor, cara menghitung vektor, cara menggambar vektor.
Penjumlahan Vektor Menggunakan Metode Grafis dan Analitis
Pernahkah Anda membayangkan jika Anda berenang di sungai searah dengan aliran sungai, kemudian Anda tiba-tiba berbalik arah 90° dari arah pergerakan semula? Apakah posisi terakhir Anda tepat sesuai keinginan Anda?
Tentu tidak, arah akhir posisi Anda tidak akan membentuk sudut 90° dari posisi semula karena terdapat hambatan arus sungai yang membuat arah gerak Anda tidak tepat atau menyimpang.
Anda dapat menentukan posisi akhir Anda dengan cara menjumlahkan vektor gerak Anda, baik perpindahannya maupun kecepatannya. Apakah Anda mengetahui cara menjumlahkan dua buah vektor? Penjumlahan vektor tidak sama dengan penjumlahan skalar.
Hal ini karena vektor selain memiliki nilai, juga memiliki arah. Vektor yang diperoleh dari hasil penjumlahan beberapa vektor disebut vektor resultan. Berikut ini akan dibahas metode-metode untuk menentukan vektor resultan.
1. Resultan Dua Vektor Sejajar
Misalnya, Anda bepergian mengelilingi kota Palu dengan mengendarai sepeda motor. Dua jam pertama, Anda bergerak lurus ke timur dan menempuh jarak sejauh 50 km. Setelah istirahat secukupnya, Anda kembali melanjutkan perjalanan lurus ke timur sejauh 30 km lagi.
Di lihat dari posisi asal, Anda telah berpindah sejauh sejauh 50 km + 30 km = 80 km ke timur. Dikatakan, resultan perpindahan Anda adalah 80 km ke timur. Secara grafis, perpindahan Anda seperti diperlihatkan pada gambar berikut ini .
 |
| Menjumlahkan dua vektor searah |
Sedikit berbeda dengan kasus tersebut, misalnya setelah menempuh jarak lurus 50 km ke timur, Anda kembali lagi ke barat sejauh 30 km. Relatif terhadap titik asal, perpindahan Anda menjadi 50 km – 30 km = 20 km ke timur. Secara grafis, perpindahan Anda diperlihatkan pada gambar berikut.
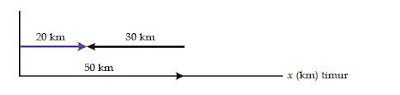 |
| Menjumlahkan dua vektor berlawanan arah |
|
|
Dari kedua contoh, seperti yang diperlihatkan pada kedua gambar diatas, menjumlahkan dua buah vektor sejajar mirip dengan menjumlahkan aljabar biasa. Secara matematis, resultan dua buah vektor sejajar, yakni, sebagai berikut. Jika vektor A dan B searah, besar vektor resultan R, adalah:
dengan arah vektor R sama dengan arah vektor A dan B. Sebaliknya, jika
kedua vektor tersebut berlawanan, besar resultannya adalah
dengan arah vektor R sama dengan arah vektor yang terbesar.
2. Resultan Dua Vektor yang Saling Tegak Lurus
Misalnya, Anda memacu kendaraan Anda lurus ke timur sejauh 40 km dan kemudian berbelok tegak lurus menuju utara sejauh 30 km.
Secara grafis, perpindahan Anda seperti diperlihatkan pada Gambar dibawah ini. Besar resultan perpindahannya, r, diperoleh menggunakan Dalil Pythagoras, yakni sebagai berikut:
Dari contoh kasus tersebut, jika dua buah vektor, A dan B, yang saling tegak lurus akan menghasilkan vektor resultan, R, yang besarnya
terhadap arah vektor A dengan catatan vektor B searah sumbu-y dan vektor A searah sumbu-x.
3. Resultan Dua Vektor yang Mengapit Sudut
Sekarang tinjau dua buah vektor, A dan B, yang satu sama lain mengapit sudut seperti yang diperlihatkan pada gambar dibawah ini (a). Gambar vektor resultannya dapat diperoleh dengan cara menempatkan pangkal vektor B di ujung vektor A.
Selanjutnya, tarik garis dari titik pangkal vektor A ke titik ujung vektor B dan buatkan panah tepat di ujung yang berimpit dengan ujung vektor B. Vektor inilah, R, resultan dari vektor A dan B. Hasilnya seperti diperlihatkan pada Gambar (b).
 |
(a) Vektor A dan vektor B mengapit sudut.
(b) Menggambarkan vektor resultan dari vektor A dan vektor B. |
Besar vektor resultan, R, dapat ditentukan secara analitis sebagai berikut. Perhatikan Gambar dibawah ini.
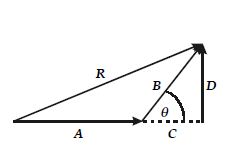 |
Menentukan besar resultan dua
buah vektor secara analitis |
Vektor C dan D diberikan sebagai alat bantu sehingga vektor A + C tegak lurus vektor D dan ketiganya membentuk resultan yang sama dengan resultan dari vektor A dan B, yakni R . Dengan menggunakan Dalil Pythagoras, besarnya vektor resultan R adalah:
4. Selisih Dua Vektor yang Mengapit Sudut
Vektor A dan vektor -A, memiliki besar yang sama, yakni |A| = |–A| = A, tetapi arahnya berlawanan seperti diperlihatkan pada Gambar berikut ini.
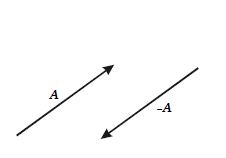 |
| Vektor A Negatif dari sebuah vektor A |
Selisih dari dua buah vektor, misalnya vektor A – B, secara grafis sama dengan jumlah antara vektor A dan vektor –B, seperti diperlihatkan pada Gambar berikut.
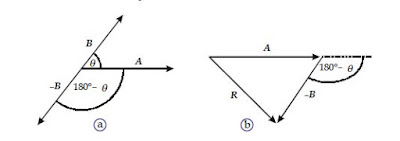 |
| Selisih dua buah vektor |
Secara matematis, vektor selisihnya ditulis R = A – B. Secara analitis, besar vektor selisihnya ditentukan dari Persamaan (2–5) dengan mengganti θ dengan 180 – θ . Oleh karena, cos (180° – θ ) = –cosθ sehingga diperoleh
5. Melukis Resultan Beberapa Vektor dengan Metode Poligon
Jika terdapat tiga buah vektor, A, B, dan C, yang besar dan arahnya berbeda seperti diperlihatkan pada Gambar (a), resultannya dapat diperoleh dengan cara menggunakan metode poligon, yakni sebagai berikut.
- Hubungkan titik tangkap vektor B pada ujung vektor A dan titik pangkal vektor C pada ujung vektor B.
- Buat vektor resultan, R, dengan titik tangkap sama dengan titik pangkal vektor A dan ujung panahnya tepat di titik ujung vektor C.
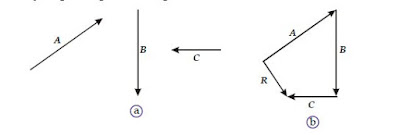 |
| Menggambarkan resultan beberapa vektor dengan metode poligon |
Secara matematis, vektor resultan pada Gambar diatas ditulis sebagai berikut.
R = A + B + C
6. Vektor Nol
Vektor nol adalah vektor hasil penjumlahan beberapa buah vektor yang hasilnya nol. Sebagai contoh, lima buah vektor, A, B, C, D, dan E, menghasilkan resultan sama dengan nol maka secara matematis ditulis:
A + B + C + D + E = 0
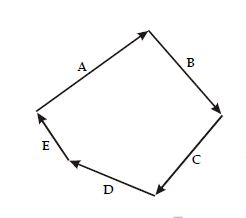 |
Penjumlahan lima buah vektor
yang menghasilkan vektor nol. |
Dengan menggunakan metode poligon, secara grafis vektor-vektor tersebut diperlihatkan seperti pada Gambar diatas. Perhatikan bahwa ujung vektor terakhir (vektor E) bertemu kembali dengan titik pangkal vektor pertama (vektor A).






